The horse, horseshoe, boots algebra puzzle got plenty of shares on social media around the time it was first published on Presh Talwalker's YouTube channel, MindYourDecisions. 

The problem goes as follows: horse plus horse plus horse equals 30; horse plus 2 horseshoes plus 2 horseshoes equals 18; 2 horseshoes minus 2 boots equals 2, and boot plus horse times horseshoe equals....what?

A lot of people are arguing over the correct answer to this algebra problem and very few seem to come to a near acceptable solution. 

The puzzle first came out in a Facebook post and has gotten over 500,000 comments (mostly guesses). Can you figure it out? 

In this video, Press Talwalker explains… 

the correct answer. 

Answers so far include 22, 23, 44, 48 and 21 – but the majority agree the correct one is 21.

The solution is reached by dividing the first number by three to get the value per horse, which is 10.

Then, on the second question subtract the horse (10) from 18 leaving you with 8 – the value of the horseshoes combined.

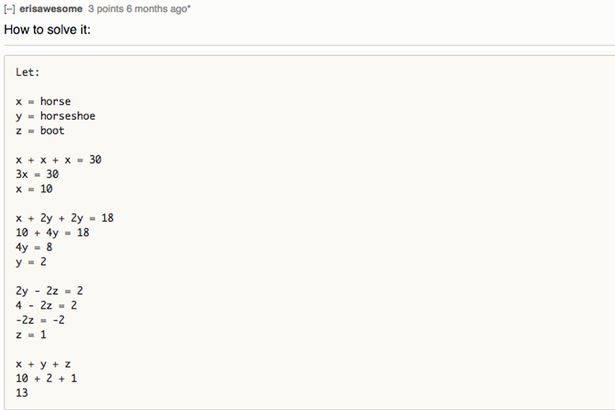
Divide that by four to get the individual value which is 2.

On the third question, the answer for two horseshoes (4) minus two cowboy boots is 2 – meaning that each boot is worth 1.

To work out the final answer you need to add a cowboy boot (1) and horse (10) and times it by a horseshoe (2).

Following the BODMAS rule – which dictates the order of operations in working out maths solutions – means you should multiply the horse by the horseshoe first (10x2) then add the cowboy boot next.

So that means the answer is 1+(10x2) = 21.

Keep in mind that the first thing you do to solve an equation is to look closely at every single detail.

For instance, the equation shows horses by the unit, but it shoes horse shoes and boots both by the unit and by the pair. 

This makes for a complicated exercise, especially if you didn’t scan it throughly.

Watch the clip below to find out the answer and compare it to the one you came up with. Share this with your friends to see if they can get it right!